How to Calculate the Specific Gravity of a Coin
[
ITA]
[ENG]
Manual
Why?
To Know the specific gravity of a coin it is useful for the
determination of its gold or silver content, this is an useful
information to discover some fakes or to study the composition of
certain coins.
Knowing the weight and volume it is possible to determine the
specific gravity (SG) of the coin, moreover if the alloy components are
known it is possible to determine with good precision the
relative
weight. Often the purity of the metal is a good sign of
authenticity.
If we want to use a simple measure of weight in order to
identify
a false coin is not a procedure that can always be right, because the
weight is the physical parameter easier to measure, and therefore it is
reproduced with absolute accuracy by forgers.
How
The experiment exploits the physical principle that a body immersed in
a liquid increases the extent of the liquid volume by an amount equal
to the volume of the body. If we know the specific weight of the liquid
we can determine the volume of the body and therefore its specific
gravity.
We take our "guinea pig" for this experiment: a Vittorio
Emanuele
II scudo 1874.
The steps are as follows:
- 1 - calibrate the scale (in this case was used a 100g step
0.01 g)
- 2 - control of the calibration (perfectly ok)
- 3 - first it is need to weigh the coin "dry", the
coin shows
no obvious signs of dust, only a slight patina.
measured weight 24.89 grams.
- 4 - construction of the suspension system for the coin
in the following pictures you can see the suspension system built with
pieces of a wooden fruit box, the wire is an ordinary sewing
thread, it is important that this should be as light as possible.
I tried to weigh the wire in water but, after carefully dipped a piece
of wire 20 times greater than that we're going to immerse with the
coin, I hadn't a considerable measure, so the wire immersed
give
as difference in weight less than 5% of 0,01 gram. We
can
consider its weight negligible.
In the images below it is possible to see the suspension system


At this point we can check the built suspension system and we can
adjust the length of the wire.
We need to get a small can of clear plastic (must be light and
transparent).
In these two pictures below we can see the coin into the jar suspended
and in the second picture, especially, we can see the coin that does
not touch any wall of the jar


At this point we can continue with the following steps:
- 5 - add distilled water in the jar (washed and cleaned if
possible), it is important to use distilled
water because it it a liquid which is known exactly the
specific
gravity. It is possible to use other liquids but we have also different
calculations.
- 6 - weight the jar with water taking care not to go over
the
capacity of the digital scale.
- 7 - tare the scale to 0 (Figure below)

- 8 - put the suspension system into the jar
at this stage we must take care that no air bubbles stay under the
coin, it can be a bit laborious, maybe try to drown the coin a
bit
tilted, taking care not to touch the water with your fingers (the
penalty it the failure of the experiment)
you can see in the figure below the coin immersed in water and the
reading of the weigh.

06
The following image is my favourite, as you can see there are no
bubbles under the coin

Now we're almost there! a bit of math will be with us until the end.
The extra weight of water with the coin submerged is: 2.41 grams (the
weight of the volume of water moved from the coin (and wire))
given the accuracy of the scale we can assume that the last weight is
between 2.405 g and 2.415 g. The same the weight of the coin
we
can consider between 24.885 and 24.895
will be useful to calculate the error.
Note: We are calculating the specific gravity, since we use distilled
water that has the same value of density (gt/cm3) if we use
another liquid the calculations are different.
Result
Well now we simply do
Coin dry weight / weight of water that have the volume of the coin =
24.89 / 2.41
specific gravity of our coin =
10.3278 g/cm³
Specific gravity of silver 900 (Latin Monetary Union):
Silver: 0.01049 g / mm ³
Copper: 0.00893 g / mm ³
Silver 900: 0.010310 g / mm ³ =
10.310
g/cm³
We have achieved something very precise:
percentage difference in
measure:
0.17%
We can now estimate the maximum error in the calculation starting from
the know error for the measure of weight:
Specific Gravity Minimum 10.3043 and maximum 10.3514
error ± 0.2%
Considerations
on accuracy
The calculation of a specific gravity of a big can be carried out, as
we have seen, with a digital scale that have an accuracy of 0,01 grams.
Such kind of digital weight can be used with coins that weight more
than 5 grams.
In table below it is possible to see the errors made using a digital
scale with an accuracy of 0,01 grams when calculating silver
coins
with a purity of 900, so with a specific gravity of 10,33 (see
next tables)
| Weight
Coin |
SGmin |
SGmax |
ERR |
| 24,89 |
10,304 |
10,351 |
0,23% |
| 12,45 |
10,281 |
10,375 |
0,45% |
| 6,22 |
10,235 |
10,423 |
0,90% |
| 3,11 |
10,143 |
10,519 |
1,79% |
| 2,51 |
10,099 |
10,566 |
2,21% |
| 1,25 |
9,880 |
10,814 |
4,34% |
| 0,63 |
9,466 |
11,344 |
8,34% |
As it is possible to see an error of 1% can give a different specific
gravity, up to 10% !
In table if a coin with a weight of 6,22 grams is taken than
it is
possible to find purity from 835 to 980: too much.
For example below the result of some measurement carried out on some
Italian coins of 5 lire of Vittorio Emanule III that have purity
of 835 and a weight of 5 grams. In chart below the squared
dots
are the result of experiment carried with a 0,01 digital scale.
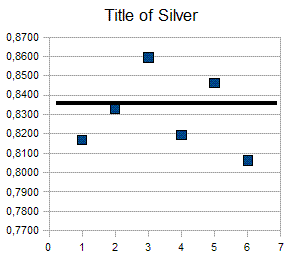 So if we want evaluate
the specific
gravity of a Roman denari or a gold zecchino we have to use a digital
scale with an accuracy of 0,001 grams.
So if we want evaluate
the specific
gravity of a Roman denari or a gold zecchino we have to use a digital
scale with an accuracy of 0,001 grams.
In table below are reported the errors we can have with a 0,001 digital
scale and with silver coin that have a purity of 900/1000 and
so
should have a specific gravity of 10,33 (see next tables)
| Weight
Coin |
Pmin |
Pmax |
ERR |
| 24,89 |
10,3255 |
10,3302 |
0,02% |
| 12,45 |
10,3231 |
10,3325 |
0,05% |
| 6,22 |
10,3184 |
10,3372 |
0,09% |
| 3,11 |
10,3090 |
10,3466 |
0,18% |
| 2,51 |
10,3045 |
10,3512 |
0,23% |
| 1,25 |
10,2814 |
10,3746 |
0,45% |
| 0,63 |
10,2353 |
10,4218 |
0,90% |
As we can see we can have great accuracy also for "small" coins.
General SG of some alloy
SG of some metals [Kg/dm³]
| Platinum |
21.37 |
| Silver |
10.492 (10.40-10.53) |
| Gold |
19.32 |
| Copper |
8.93 |
| lead |
11.24 |
| Zinc |
7.13 (7.04-7.16) |
| Tin |
7.29 |
| Nikel |
8.02 |
| Cadmium |
8,648 |
For Alloy we have to calculate the percentage in weight of the mail
metal against the other alloy composition.
For example if a SG of a denarius of Titus is found to be
10.4,
meaning it
contains 94% silver and 6% copper and impurities.
SG of some alloys, calculated values (Gold with copper, Silver
with copper, Copper with Zinc and Copper with Tin)
|
Purity 100% |
Purity 98% |
Purity 90% |
Purity 835% |
Purity 75% |
Purity 50% |
| Gold |
19.30 |
18.86 |
17.29 |
16.20 |
14.96 |
12.21 |
| Silver |
10.49 |
10.45 |
10.31 |
10.20 |
10.05 |
9.65 |
| Copper (+Zinc) |
8.93 |
8.89 |
8.71 |
8.57 |
8.40 |
7.93 |
| Copper (+Tin) |
8.93 |
8.89 |
Bronze
8.73 |
Bronze -asses
8.61 |
Orichalcum -
Sestertii and dupondii
8.46 |
White alloy
used for many fakes
8.03 |
Other information can be found in
'The Specific Gravity of the Gold Coins of
Aksum' by W. A. Oddy and S. C. Monro-Hay in 'Metallurgy in Numismatics'
by Metcalf and Oddy, 1980.
This paper showed
gold of 94% = SG of 18.5,
92% = SG 18.15,
91% = SG of 18.01.
Also 'The Chemical
composition of Parthian Coins' by E. R. Caley, chapter VII in
'Numismatic Notes and Monographs' #129, ANS, 1955, which has a Table
XXIV, of silver content related to SG. Some figures from that
chart are;
99% silver = SG 10.48,
95% =
10.41,
86% = 10.24,
75% = SG 10.05.
Thanks to Marvin of Moneta-L for this data.
Plese remember that in many gold coins the know gold content in the
alloy can be found to be with an error of +/- 2,0%.
Possible errors in the experiment
weight of the wire:
we demonstrated that the weight of the wire give an error less than
0.0005 grams
specific gravity of water:
the specific gravity of a body changes with temperature, the specific
weight of distilled water at 4 degrees is 1.0000 g/cm³
the specific gravity of water at 20 degrees is 0.9982 g/cm³
there is therefore an error of about ± 0.18% in the calculation,
although we can correct it only by calculation
for maximum accuracy, the coin should be cleaned and degreased, as is
feasible without major problems on gold is not on silver coins that
could be ruined if patina is taken away.
becomes difficult to resolve the problem mathematically in the case of
three or more metal alloys, the only viable solution is the use of XRF
spectrometry (X-ray Fluorescence) (but that give indication
of alloy composition only of the most surface layer of the coin). With
an alloy of three metals, if we
do not know any of the three ratios we should solve two equations with
three unknowns and this is not possible, however, we could take same
assumptions and calculate the possible error to see how this could
affect the result.
For many ancient silver coins
like antoninianus, Alexander tetradracms, etc. namely coins
that are not in simple binary alloy, the result would be just a
number to be interpreted, and can be used at least, for comparative
tests.
Also for Republican and Imperial denarii sometimes you might make
a wrong measure. While ignoring the trace of other elements, should be
considered, as example, that a lot of denarii may contain gold
percentages to 0.7-0.9% and in other cases lead to over 6%.
For example
denariA: Ag 90% -
Cu 10% = specific gravity 10.310 g/cm³ (theoretical)
denariB: Ag 80% -
Cu 13% - Pb 7% = specific gravity 10.304 g/cm³ (theoretical)In practice, the results must always be interpreted and not used as the
verdicts on the coins analysed.
If you analyse gold and silver having a high title, say above 95% then
the results can be accurate and can give us a good indication of the
alloy of the coin. Gradually, the title of principal metal decreases
the results are increasingly inaccurate. Coins that have low gold
content would not give such great signs from their specific gravity
because we do not know the proportion of other metals in the alloy.
Conclusion:
The
proposed method it is useful to calculate with good accuracy
the
specific gravity of a coin, applies to antique and modern
coins, and it is not at all destructive.
A really useful tool in
the hands of
enthusiasts and professionals to get a good indication of the specific
gravity of the coin that is going to be studied!
Alessandro
Attila the collector
Note
Use of another liquid for the measure.
to avoid generation of bubbles in our weight experiment we can use a
different liquid insted demineralized water. We have to keep in account
the different specific gravity of the new liquid we are going to use.
with the following notations
Pm weight of the coin
Vm volume of the coin = volume of liquid moved by the coin body
Pq weight of the liquid with the same volume of the coin
Psq Specific gravity of the liquid
in a case of a generic liquid we have
Psm = Pm /Vm
weighting the liquid moved by the body of the coin:
Vm = Pq / Psq
so
Psm = Pm * Psq / Pq
so we can see why when we use distilled water with a specific gravity
equal to 1 the formula became Ps = Pm / Pq
if for example we use ethanol at 95% that have a specific gravity of
0,81 the formula to use get the following:
Ps = Pm * 0,81 / Pq
A different solution is to wet the coin in alcohol, the
adherence of alcohol to coin is, we would
dare to say, far less than volume of the thread that hangs the coin. On
the other side, alcohol mixes with water, and is only measured the
volume (well, weight) of coin.
One could use indeed ethanol, but
that involves some troubles, like it is very
sensitive to increases/decreases in temperature
Also we could use
de-mineralized water with a drop of tensioactive, being the best
dioctylsodiumsulfosuccinate (aerosol OT is a commercial brand). But
that
is not that easy to get.
Finally we can simply add a drop of the dishwasher we use generally.
Use of a little dish for the weight:
we could use a little transparent dish where we could place the coin we
are going to weight. We always be careful to avoid bubbles between dish
and coin, for little coins can be useful to submerge before the little
dish and then "diving" over the coin being careful do not touch the
water.
Note on specific gravity of a alloy
we assume that the specific gravity of alloy composition
is given on mass and not in volume. This is not correct but in case of
two metals the error is negligible.
If we assume that a coin is made of two metals we could calculate the
title.
For example:
is X the silver tile of a coin made with silver and copper
is P and V the coin weight and volume
is Ps the specific gravity, measured with our system, of the coin
Parg and Pram the weights respectively of silver and copper in the coin.
Psarg and Psram the specific gravity respectively of silver and copper.
then
P = Parg + Pram = Psarg * Varg + Psram * Vram = Parg * V * X + Psram *
V * (1-X)
so considering P/V =Ps
Psarg * X + Psram * (1-X) = Ps
that with simple maths operations
X = (Ps-Psram)/(Psarg - Psram)
Note attached: demonstration that
from calculation of
diameter and thickness we do not get the volume of the coin
I take one of the Scudo coin I have and I measure the following data:
Diameter: 37 mm
Thickness: 2.5 mm
The thickness was measured at the edge with a micrometer that
appreciates the tenth of a millimetre.
Unfortunately I can not measure well the thickness at the fields but I
note that the thickness at the field is near to 2.35 mm
Now:
the surface of the coin is 3.14 · D² / 4 = 1075.21 mm²
then
Volume = 2688.03 mm ³
Well at this point I report the specific gravities of the content
metals of the coin:
Silver: 0.01049 g / mm ³
Copper: 0.00893 g / mm ³
Please note however that the specific gravity of alloy
composition
is given on mass and not in volume. Ie every 100 grams of Ag900 90
grams are silver and 10 grams copper. If we make
the calculation
of the specific gravity with volume ratio we would have an
approximation because the assumption that the total volume of
the
alloy is equal to the volume of the two separated metals is not always
true, however in this case the error would be not so high. In any case
if we do the calculation using volume ratios we reach a very
close result, it is not the sore point.
With a bit of calculations by solving two equations with two unknowns
(omitted here)
our result:
Volume occupied by silver: 2377.69 mm ³
Volume occupied by copper: 310.34 mm ³
Multiply the Specific Gravity for the volume just found:
SG x Volume occupied by silver = weight of silver
Silver weight: 24.94 g
Copper weight: 2.77 g
The sum is 27.71 grams
Ok ok, you can say that the problem is simply the measure of the
thickness of the coin. Probably, but I did the calculation for the
correct value and we should measured a thickness of 2.255 mm
but
it would be too much, even below the surface of the field, to try again
I did this analysis with 5 Lira 1927 little eagle Italy and the result
is that I should have a thickness of 1.18 mm instead of 1.68 correctly
measured (we are really out here)
then this technique is wrong and can not be used for the calculation of
a coin volume.
Alessandro Attila the collector
Bibliograpy
Home
of Attila Coin
Site







 06
06